LSTM

Why do we need LSTM?

1. RNNs, Although take past ‘context’ into consideration. They do suffer the problem of Vanishing or Exploding gradient problem. Simply put, the gradient is calculated in any neural network using backpropogation which computes the derivate of a network backpropogating through each layer of the network. In order to update the weight matrix we need to compute the derivative of Loss w.r.t. the weight . Chain rule plays a key role in calculating derivative of initial layer as the derivative of subsequent layers are multiplied in order to calculate the gradient. However, for considerably large networks, this creates a problem.As the activation function output the values compressed beteen 0 and 1 for example sigmoid function, as we back propogate the network, the value of gradient d(sigmoid output) / d(affine output (WXt +bias)) could attai very small value close to 0 and when these values are multipled using chain rule, the the actual gradient for the inital layers become very small rendering the network stagnant in terms of weight updation. Check Backpropogation for more.
2. One more problem specifically with RNNs is that they are not able to preserve context for long sequences. As the length of input sequence grows, the ‘context carrying’ ability of RNNs takes a toll. Why you may ask? Well, the reason being that despite having access to the entire preceding sequence, the information encoded in hidden states tends to be fairly local, more relevant to the most recent parts of the input sequence and recent decisions. Yet distant information is critical to many language applications. Consider the following example in the context of language modeling. The flights the airline was cancelling were full.

Assigning a high probability to was following airline is straightforward since airline provides a strong local context for the singular agreement. However, assigning an appropriate probability to were is quite difficult, not only because the plural flights is quite distant, but also because the intervening context involves singular constituents. Ideally, a network should be able to retain the distant information about plural flights until it is needed, while still processing the intermediate parts of the sequence correctly. One reason for the inability of RNNs to carry forward critical information is that the hidden layers, and, by extension, the weights that determine the values in the hidden layer, are being asked to perform two tasks simultaneously: provide information useful for the current decision, and updating and carrying forward information required for future decisions.

---

What is LSTM?

LSTM is an acronym for Long Short Term Memory networks which addresses and solves the above stated problem with RNNs.

LSTMs divide the context management problem into two subproblems:

1. removing information no longer needed from the context,
2. and adding information likely to be needed for later decision making.

The key to solving both problems is to learn how to manage this context rather than hard-coding a strategy into the architecture. LSTMs accomplish this by first adding an explicit context layer to the architecture in addition to the usual recurrent hidden layer, and through the use of specialised neural units that make use of gates to control the flow of information into and out of the units that comprise the network layers. These gates are implemented through the use of additional weights that operate sequentially on the input, and previous hidden layer, and previous context layers.

---

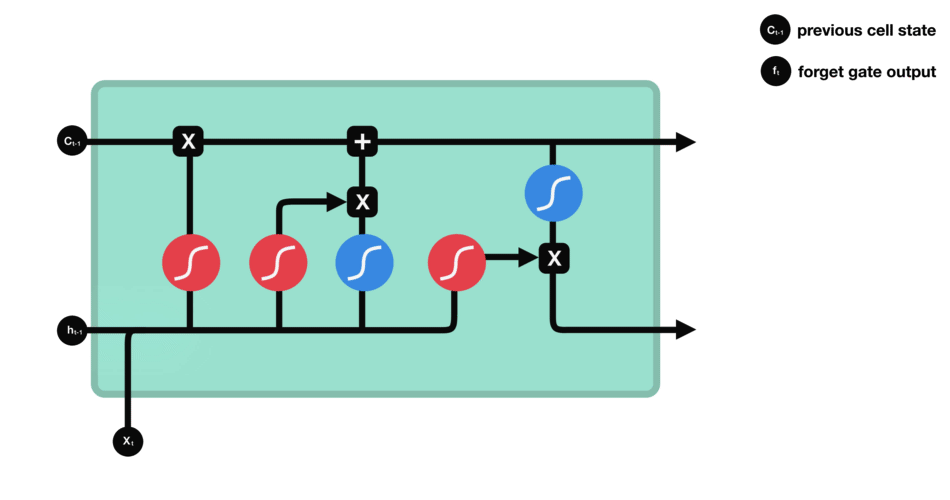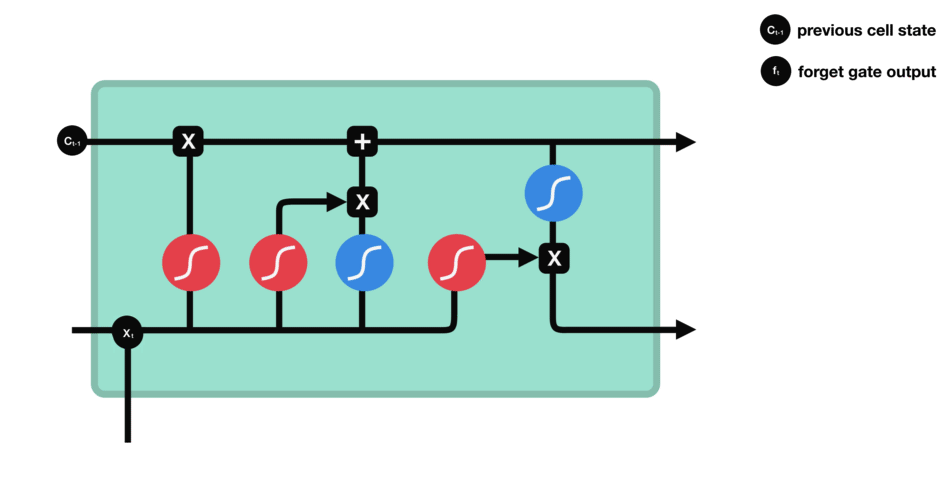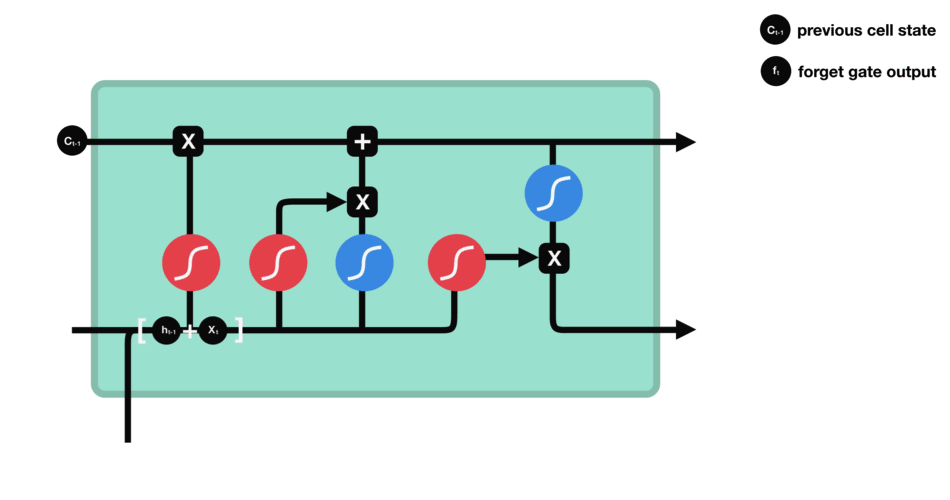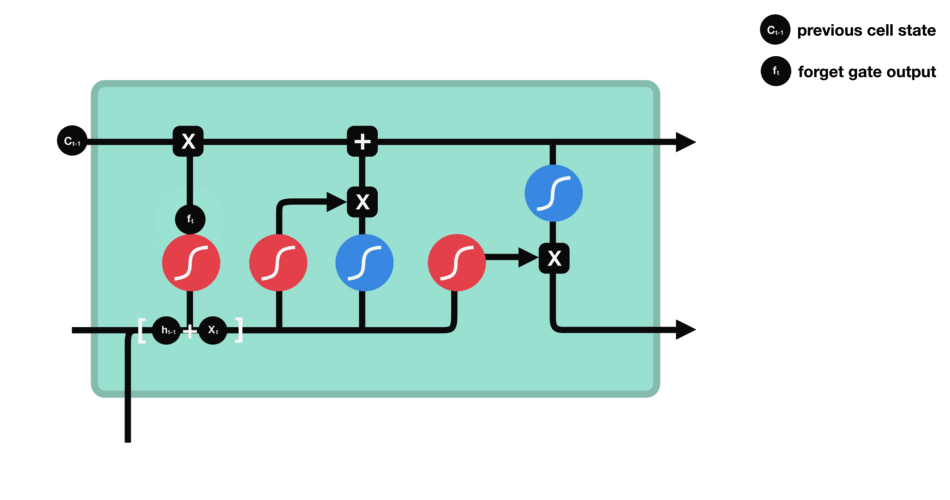
Architecture:

The gates in an LSTM share a common design pattern; each consists of a feedforward layer, followed by a sigmoid activation function, followed by a pointwise multiplication with the layer being gated. The choice of the sigmoid as the activation function arises from its tendency to push its outputs to either 0 or 1. Combining this with a pointwise multiplication has an effect similar to that of a binary mask. Values in the layer being gated that align with values near 1 in the mask are passed through nearly unchanged; values corresponding to lower values are essentially erased.

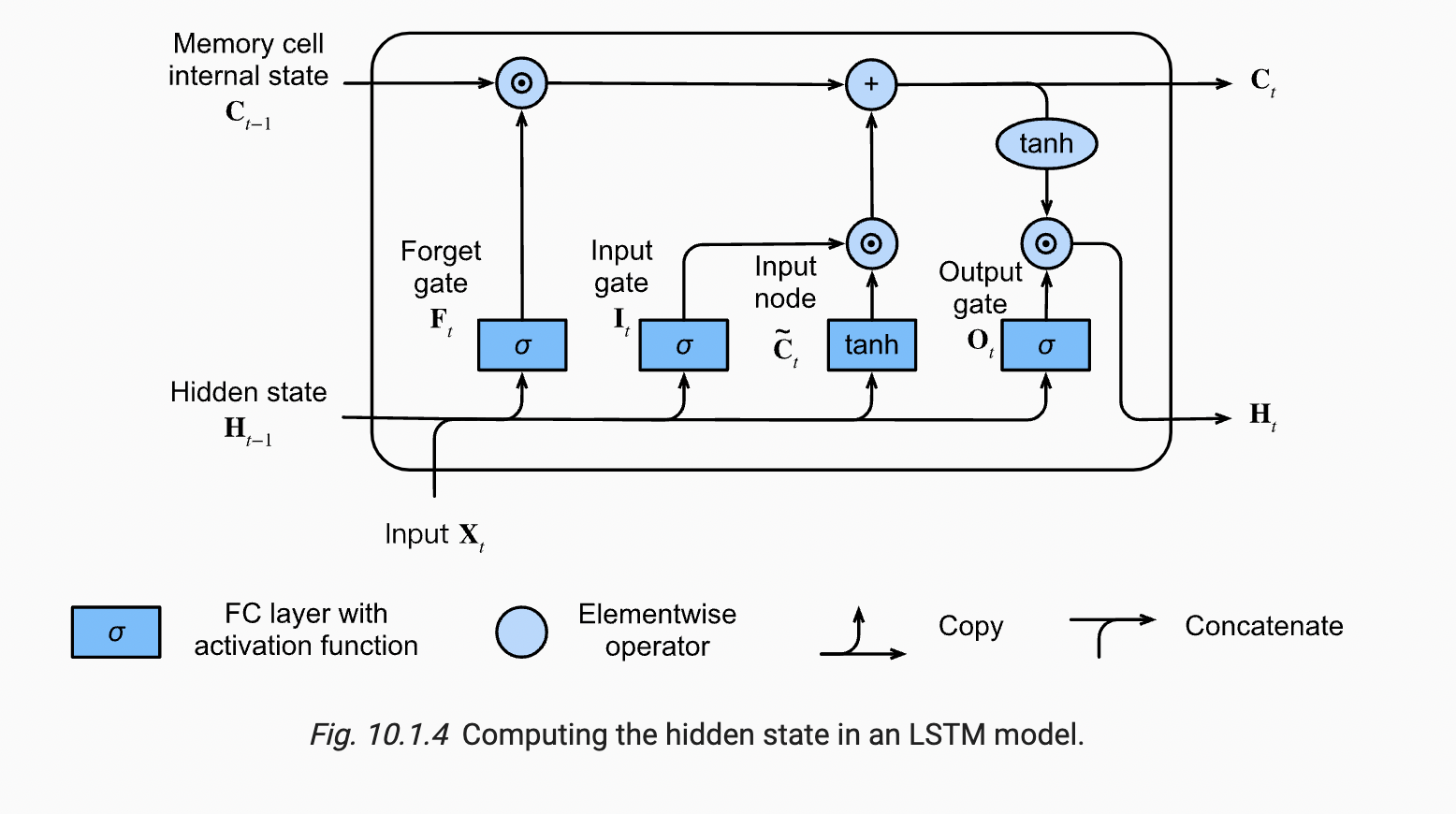
An LSTM cell receives 3 inputs. X or input vector at time=t . A hidden vector h(t-1) along with a new context vector c(t-1) also sometimes referred to as cell state. With these 3 inputs, LSTM cell performs few operations discussed later in this post to perform transformations/updations of the cell state C(t) and h(t) and produce output vector O(t). For simplicity, let’s keep in mind that C(t) is basically Long Term Memory of the network while h(t) is the Short Term Memory. Now the name LSTM is beginning to make sense.

In practice, the LSTM unit uses recent past information (the short-term memory, H) and new information coming from the outside (the input vector, X) to update the long-term memory (cell state, C). Finally, it uses the long-term memory (the cell state, C) to update the short-term memory (the hidden state, H). The hidden state determined in instant t is also the output of the LSTM unit in instant t. It is what the LSTM provides to the outside for the performance of a specific task. In other words, it is the behaviour on which the performance of the LSTM is assessed.

Below diagram for a single LSTM cell introduces few advances over the existing vanilla RNNs.

source

Let’s dive into each subpart of the cell.

1. Forget gate:

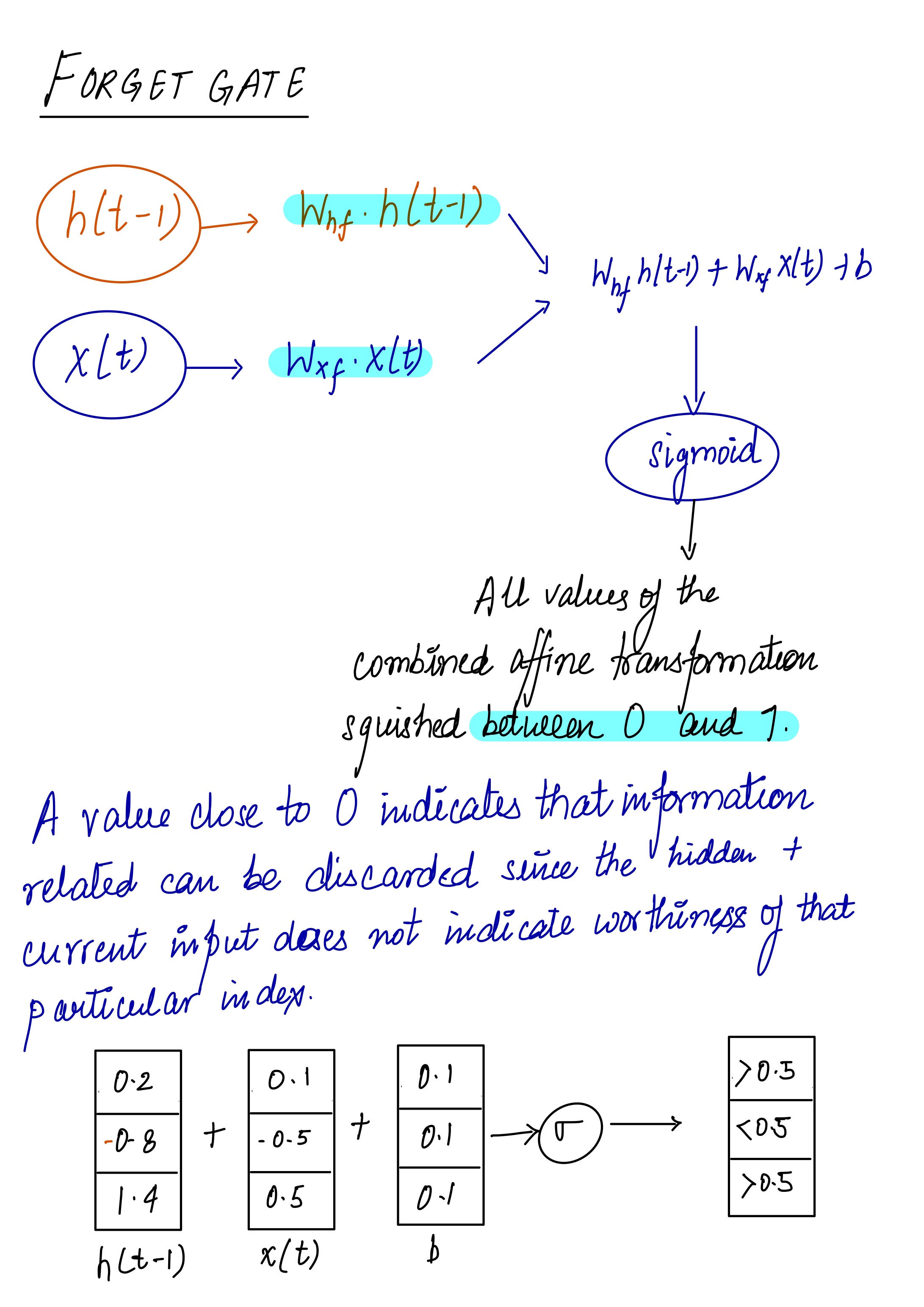
The purpose of this gate is to ‘forget’ or delete the irrelevant bit of the historical context which is no longer required. The forget gate computes a weighted sum of the previous state’s hidden layer and the current input and passes that through a sigmoid. This mask is then multiplied element-wise by the context vector to remove the information from context that is no longer required. Element-wise multiplication of two vectors represented by the operator , and sometimes called the Hadamard product is the vector of the same dimension as the two input vectors, where each element i is the product of element i in the two input vectors. The corresponding equation for the forget gate is as given below

$$\begin{split}\begin{aligned} \mathbf{I}_t &= \sigma(\mathbf{X}_t \mathbf{W}_{xi} + \mathbf{H}_{t-1} \mathbf{W}_{hi} + \mathbf{b}_i),\\ \mathbf{F}_t &= \sigma(\mathbf{X}_t \mathbf{W}_{xf} + \mathbf{H}_{t-1} \mathbf{W}_{hf} + \mathbf{b}_f),\\ \mathbf{O}_t &= \sigma(\mathbf{X}_t \mathbf{W}_{xo} + \mathbf{H}_{t-1} \mathbf{W}_{ho} + \mathbf{b}_o), \end{aligned}\end{split}$$

where 

$\mathbf{W}_{xi}, \mathbf{W}_{xf}, \mathbf{W}_{xo} \in \mathbb{R}^{d \times h}$

and

$\mathbf{W}_{hi}, \mathbf{W}_{hf}, \mathbf{W}_{ho} \in \mathbb{R}^{h \times h}$

are weight parameters and 

$\mathbf{b}_i, \mathbf{b}_f, \mathbf{b}_o \in \mathbb{R}^{1 \times h}$

are bias parameters.

So under the hood, what exactly happening is weighted sum of current input and previous hidden state along with the bias is passed through a fully connected layer and then to a sigmoid function.

The output of sigmoid function is again multiplied with previous cell state C(t-1) in a pointwise multiplication fashion.

If we look closely at the cell state in architecture diagram, Cell state doesn’t go through any feed forward layer, it acts like a gateway to carry information through each cell to the next one. Which means it never gets to interact with any weight matrix and hence doesn’t suffer with Vanishing/Exploding gradient problem.

Bla bla bla! but what do you mean it ‘forgets’ information?

Well, Forget gate does two operations under the hood. Firstly, it combines the hidden state from previous cell which is nothing but historical context carried over time with the current input. Forget gate has to ‘think’ which information should it retain from current input based on past historical context. While reading a research or a news article, we do not remember entire sequence of words. While reading a sentence, our understanding or interpretation of the current sentence is build upon the information we carried from the first word itself.

In a similar fashion, a typical forget gate in a LSTM cell receives current input ‘I won’t be able to make it to the party’ and aligns this sentence with the first sentence in this example text which could be ‘I am feeling sick today’. Based on past state, the information related to ‘feeling sick’ tells the forget gate to remember ‘No Party today’ and forget everything else such as ‘I, am, make’ etc.

Neural networks do not consume data like the way I discussed above, usually for NLP tasks data words is converted into fixed length embeddings. But above example is the most intuitive explanation I could find.

Mathematically speaking above ‘forget’ operation is performed by looking at the past hidden state h(t-1) and current input x(t) . An affine transformation of both the states is passed over to a sigmoid function.

The resultant matrix from sigmoid is multiplied elementwise with the current state C(t) (carried forward) which updates the current state with information forget gate suggested to remember or forget.

1. Input gate and Input Node:

   Input gate and Input node is responsible for checking the current input and determining what information is worth keeping and updates the current state with that information.

Again the concatenated/affined version of current input and previous hidden state along with the bias is calculated . But there is a slight variation in this part, this weighted sum is fed parallel to two separate functions , sigmoid and tanh . Both the outputs are again multiplied elementwise

I am working on details of LSTM. More details will be updated soon.

Sources:

LSTM Simply Explained

How Backprop works

Arxiv Paper on LSTM

---